16) HW2 solution#
We want to solve the matrix multiplication problem
\[
C := C + A B^{T}. \qquad \qquad \qquad \qquad \hbox{(1)}
\]
Here \(A\), \(B\), and \(C\) have sizes \(m \times k\), \(n \times k\), and \(m \times n\), respectively. Using the same notation that we’ve seen in class, where capital letters are typically for matrices, and lower case Greek letters for floating point scalars: \(\alpha\) (for entries of the matrix \(A\)), \(\beta\) (for entries of the matrix \(B\)), and \(\gamma\) (for entries of the matrix \(C\)).
Recognizing that the \(pj\) element of \(B^{T}\) is the \(jp\) element of \(B\), it follows that the \(ij\) element of \(C\) can be computed as
\[
\gamma_{ij} := \gamma_{ij} + \sum_{p = 1}^{k} \alpha_{ip} \beta_{jp}.
\]
# matrix times row vector (update rows of `C`) with inner dot product
function mygemm_ijp!(C, A, B)
m, k = size(A)
_, n = size(B)
@assert size(B, 1) == k
@assert size(C) == (m, n)
for i = 1:m
for j = 1:n
for p = 1:k
@inbounds C[i, j] += A[i, p] * B[j, p]
end
end
end
end
# matrix times row vector (update rows of `C`) with inner axpy
function mygemm_ipj!(C, A, B)
m, k = size(A)
_, n = size(B)
@assert size(B, 1) == k
@assert size(C) == (m, n)
for i = 1:m
for p = 1:k
for j = 1:n
@inbounds C[i, j] += A[i, p] * B[j, p]
end
end
end
end
# Rank one update (repeatedly update all elements of `C`) with outer product
# using axpy with rows of `B`
function mygemm_pij!(C, A, B)
m, k = size(A)
_, n = size(B)
@assert size(B, 1) == k
@assert size(C) == (m, n)
for p = 1:k
for i = 1:m
for j = 1:n
@inbounds C[i, j] += A[i, p] * B[j, p]
end
end
end
end
# Rank one update (repeatedly update all elements of `C`) with outer product
# using axpy with columns of `A`
function mygemm_pji!(C, A, B)
m, k = size(A)
_, n = size(B)
@assert size(B, 1) == k
@assert size(C) == (m, n)
for p = 1:k
for j = 1:n
for i = 1:m
@inbounds C[i, j] += A[i, p] * B[j, p]
end
end
end
end
# matrix times column vector (update columns of `C`) with inner axpy
function mygemm_jpi!(C, A, B)
m, k = size(A)
_, n = size(B)
@assert size(B, 1) == k
@assert size(C) == (m, n)
for j = 1:n
for p = 1:k
for i = 1:m
@inbounds C[i, j] += A[i, p] * B[j, p]
end
end
end
end
# matrix times column vector (update columns of `C`) with inner dot product
function mygemm_jip!(C, A, B)
m, k = size(A)
_, n = size(B)
@assert size(B, 1) == k
@assert size(C) == (m, n)
for j = 1:n
for i = 1:m
for p = 1:k
@inbounds C[i, j] += A[i, p] * B[j, p]
end
end
end
end
mygemm_jip! (generic function with 1 method)
## Testing
# What modules / packages do we depend on
using Random
using LinearAlgebra
using Printf
using Plots
default(linewidth=4) # Plots embelishments
# To ensure repeatability
Random.seed!(777)
# Don't let BLAS use lots of threads (since we are not multi-threaded yet!)
BLAS.set_num_threads(1)
include("../julia_codes/hw2_sol/mygemm.jl")
# C := α * A * B + β * C
refgemm!(C, A, B) = mul!(C, A, B', one(eltype(C)), one(eltype(C)))
# matrix times row vector (update rows of `C`) with inner dot product
# mygemm! = mygemm_ijp!
# matrix times row vector (update rows of `C`) with inner axpy
# mygemm! = mygemm_ipj!
# Rank one update (repeatedly update all elements of `C`) with outer product
# using axpy with rows of `B`
# mygemm! = mygemm_pij!
# Rank one update (repeatedly update all elements of `C`) with outer product
# using axpy with columns of `A`
mygemm! = mygemm_pji!
# matrix times column vector (update columns of `C`) with inner axpy
# mygemm! = mygemm_jpi!
# matrix times column vector (update columns of `C`) with inner dot product
# mygemm! = mygemm_jip!
num_reps = 3
# What precision numbers to use
FloatType1 = Float32
FloatType2 = Float64
@printf("size | reference | %s\n", mygemm!)
@printf(" | seconds GFLOPS | seconds GFLOPS diff\n")
N = 48:48:480
best_perf = zeros(length(N))
# Size of square matrix to consider
for nmk in N
i = Int(nmk / 48)
n = m = k = nmk
@printf("%4d |", nmk)
gflops = 2 * m * n * k * 1e-09
# Create some random initial data
A = rand(FloatType1, m, k)
B = rand(FloatType1, n, k)
C = rand(FloatType1, m, n)
# Make a copy of C for resetting data later
C_old = copy(C)
# "truth"
C_ref = A * B' + C
# Compute the reference timings
best_time = typemax(FloatType1)
for iter = 1:num_reps
# Reset C to the original data
C .= C_old;
run_time = @elapsed refgemm!(C, A, B);
best_time = min(run_time, best_time)
end
# Make sure that we have the right answer!
@assert C ≈ C_ref
best_perf[i] = gflops / best_time
# Print the reference implementation timing
@printf(" %4.2e %8.2f |", best_time, best_perf[i])
# Compute the timing for mygemm! implementation
best_time = typemax(FloatType1)
for iter = 1:num_reps
# Reset C to the original data
C .= C_old;
run_time = @elapsed mygemm!(C, A, B);
best_time = min(run_time, best_time)
end
best_perf[i] = gflops / best_time
# Compute the error (difference between our implementation and the reference)
diff = norm(C - C_ref, Inf)
# Print mygemm! implementations
@printf(" %4.2e %8.2f %.2e", best_time, best_perf[i], diff)
@printf("\n")
end
plot!(N, best_perf, xlabel = "m = n = k", ylabel = "GFLOPs/S", label = "$mygemm! $FloatType1", title = "Float32 Vs Float64")
## FloatType2
@printf("size | reference | %s\n", mygemm!)
@printf(" | seconds GFLOPS | seconds GFLOPS diff\n")
N = 48:48:480
best_perf = zeros(length(N))
# Size of square matrix to consider
for nmk in N
i = Int(nmk / 48)
n = m = k = nmk
@printf("%4d |", nmk)
gflops = 2 * m * n * k * 1e-09
# Create some random initial data
A = rand(FloatType2, m, k)
B = rand(FloatType2, n, k)
C = rand(FloatType2, m, n)
# Make a copy of C for resetting data later
C_old = copy(C)
# "truth"
C_ref = A * B' + C
# Compute the reference timings
best_time = typemax(FloatType2)
for iter = 1:num_reps
# Reset C to the original data
C .= C_old;
run_time = @elapsed refgemm!(C, A, B);
best_time = min(run_time, best_time)
end
# Make sure that we have the right answer!
@assert C ≈ C_ref
best_perf[i] = gflops / best_time
# Print the reference implementation timing
@printf(" %4.2e %8.2f |", best_time, best_perf[i])
# Compute the timing for mygemm! implementation
best_time = typemax(FloatType2)
for iter = 1:num_reps
# Reset C to the original data
C .= C_old;
run_time = @elapsed mygemm!(C, A, B);
best_time = min(run_time, best_time)
end
best_perf[i] = gflops / best_time
# Compute the error (difference between our implementation and the reference)
diff = norm(C - C_ref, Inf)
# Print mygemm! implementations
@printf(" %4.2e %8.2f %.2e", best_time, best_perf[i], diff)
@printf("\n")
end
plot!(N, best_perf, xlabel = "m = n = k", ylabel = "GFLOPs/S", label = "$mygemm! $FloatType2", title = "Float32 Vs Float64")
size | reference | mygemm_pji!
| seconds GFLOPS | seconds GFLOPS diff
48 | 5.97e-06 37.03 |
1.93e-05 11.45 4.77e-06
96 | 3.14e-05 56.27 | 9.98e-05 17.73 1.72e-05
144 | 9.10e-05 65.65 | 3.07e-04 19.48 2.67e-05
192 | 2.03e-04 69.73 | 6.43e-04 22.01 3.81e-05
240 | 3.79e-04 72.88 | 1.28e-03 21.68 5.34e-05
288 | 6.34e-04 75.31 | 2.78e-03 17.18 8.39e-05
336 | 1.16e-03 65.23 | 6.23e-03 12.18 1.14e-04
384 | 1.72e-03 65.76 | 9.07e-03 12.49 1.45e-04
432 | 2.42e-03 66.61 |
1.24e-02 12.97 1.68e-04
480 | 2.91e-03 76.08 |
1.45e-02 15.24 1.83e-04
size | reference | mygemm_pji!
| seconds GFLOPS | seconds GFLOPS diff
48 | 1.12e-05 19.76 |
2.65e-05 8.36 5.33e-15
96 | 5.76e-05 30.71 | 1.62e-04 10.94 1.42e-14
144 | 1.75e-04 34.03 | 5.08e-04 11.76 2.84e-14
192 | 4.72e-04 29.99 | 1.98e-03 7.13 2.84e-14
240 | 8.49e-04 32.55 | 4.12e-03 6.71 4.26e-14
288 | 1.34e-03 35.78 | 6.55e-03 7.29 1.85e-13
336 | 1.94e-03 39.01 |
9.87e-03 7.68 2.13e-13
384 | 2.83e-03 40.02 | 1.48e-02 7.66 2.56e-13
432 | 3.93e-03 41.07 |
2.10e-02 7.66 3.41e-13
480 | 6.24e-03 35.44 |
2.88e-02 7.67 3.41e-13
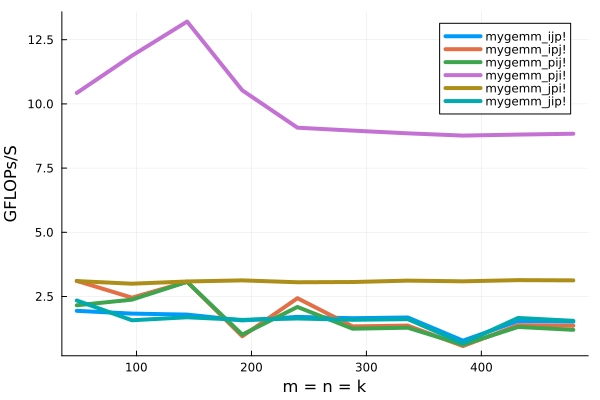
By uncommenting each of the individual my_gemm with the different loop orderings in the above code, for Float64 precision, we find that the best loop ordering for this problem is pji. Notice that Julia stores matrices in clumn-major order and data in columns are stored contiguously. The pji loop ordering performs a rank-one update (it repeatedly updates all elements of \(C\)) with outer product computed using axpy with the column vector \(a_p\).
\[
a_{p} \tilde{b}_{p}^T =
\begin{bmatrix}
a_{p} \beta_{1p} & \cdots & a_{p} \beta_{mp}
\end{bmatrix}
\]
In the code snippet
for p = 1:k
for j = 1:n
for i = 1:m
@inbounds C[i, j] += A[i, p] * B[j, p]
end
end
end
being i the fastest index, each execution of the inner-most loop traverses the \(p\)-th column of \(A\), \( a_{p}\), multiplies it by the \(\beta_{jp}\) entry of \(B\) (moving down in the column entries at the next iteration of the j loop, facilitating cache reuse), and updates columns of \(C\).
The following numbers are the result of the executions on my machine:
size | reference | mygemm_ijp!
| seconds GFLOPS | seconds GFLOPS diff
48 | 8.01e-06 27.60 | 1.12e-04 1.97 7.11e-15
96 | 4.83e-05 36.66 | 9.83e-04 1.80 1.78e-14
144 | 1.46e-04 40.88 | 3.45e-03 1.73 2.84e-14
192 | 3.58e-04 39.55 | 8.47e-03 1.67 3.55e-14
240 | 6.21e-04 44.56 | 1.66e-02 1.67 5.68e-14
288 | 1.04e-03 45.74 | 2.91e-02 1.64 1.71e-13
336 | 1.65e-03 45.98 | 4.57e-02 1.66 2.27e-13
384 | 2.47e-03 45.87 | 1.57e-01 0.72 2.70e-13
432 | 3.63e-03 44.47 | 9.70e-02 1.66 2.84e-13
480 | 6.10e-03 36.26 | 1.53e-01 1.45 3.69e-13
size | reference | mygemm_ipj!
| seconds GFLOPS | seconds GFLOPS diff
48 | 8.06e-06 27.46 | 6.83e-05 3.24 7.11e-15
96 | 4.79e-05 36.91 | 7.54e-04 2.35 1.78e-14
144 | 1.45e-04 41.06 | 1.84e-03 3.25 2.84e-14
192 | 5.21e-04 27.15 | 1.07e-02 1.33 3.55e-14
240 | 6.73e-04 41.10 | 1.11e-02 2.49 5.68e-14
288 | 1.04e-03 45.78 | 3.44e-02 1.39 1.71e-13
336 | 1.64e-03 46.33 | 5.30e-02 1.43 2.27e-13
384 | 2.44e-03 46.42 | 1.85e-01 0.61 2.70e-13
432 | 3.58e-03 45.06 | 1.13e-01 1.43 2.84e-13
480 | 5.58e-03 39.60 | 1.60e-01 1.38 3.69e-13
size | reference | mygemm_pij!
| seconds GFLOPS | seconds GFLOPS diff
48 | 8.06e-06 27.45 | 6.95e-05 3.18 7.11e-15
96 | 4.83e-05 36.66 | 6.73e-04 2.63 1.78e-14
144 | 1.46e-04 40.84 | 1.92e-03 3.10 2.84e-14
192 | 3.30e-04 42.90 | 1.15e-02 1.24 3.55e-14
240 | 8.77e-04 31.52 | 1.62e-02 1.71 5.68e-14
288 | 1.95e-03 24.56 | 3.74e-02 1.28 1.71e-13
336 | 1.65e-03 45.88 | 5.72e-02 1.33 2.27e-13
384 | 2.62e-03 43.23 | 1.83e-01 0.62 2.70e-13
432 | 4.90e-03 32.88 | 1.23e-01 1.31 2.84e-13
480 | 5.94e-03 37.23 | 1.75e-01 1.26 3.69e-13
size | reference | mygemm_pji!
| seconds GFLOPS | seconds GFLOPS diff
48 | 8.02e-06 27.58 | 2.07e-05 10.67 7.11e-15
96 | 4.79e-05 36.91 | 1.35e-04 13.10 1.78e-14
144 | 1.46e-04 40.96 | 4.31e-04 13.86 2.84e-14
192 | 3.28e-04 43.12 | 1.21e-03 11.65 3.55e-14
240 | 1.04e-03 26.66 | 3.47e-03 7.96 5.68e-14
288 | 1.08e-03 44.19 | 5.37e-03 8.90 1.71e-13
336 | 1.71e-03 44.50 | 8.59e-03 8.84 2.27e-13
384 | 2.46e-03 46.06 | 1.28e-02 8.84 2.70e-13
432 | 3.52e-03 45.80 | 1.82e-02 8.87 2.84e-13
480 | 4.66e-03 47.48 | 2.52e-02 8.79 3.69e-13
size | reference | mygemm_jpi!
| seconds GFLOPS | seconds GFLOPS diff
48 | 8.22e-06 26.92 | 6.79e-05 3.26 7.11e-15
96 | 4.81e-05 36.81 | 5.03e-04 3.51 1.78e-14
144 | 1.46e-04 40.87 | 1.80e-03 3.31 2.84e-14
192 | 3.43e-04 41.29 | 4.41e-03 3.21 3.55e-14
240 | 6.30e-04 43.89 | 8.90e-03 3.11 5.68e-14
288 | 1.44e-03 33.24 | 1.69e-02 2.83 1.71e-13
336 | 1.66e-03 45.60 | 2.48e-02 3.06 2.27e-13
384 | 2.46e-03 46.03 | 3.52e-02 3.22 2.70e-13
432 | 5.47e-03 29.50 | 4.89e-02 3.30 2.84e-13
480 | 5.36e-03 41.30 | 6.70e-02 3.30 3.69e-13
size | reference | mygemm_jip!
| seconds GFLOPS | seconds GFLOPS diff
48 | 8.03e-06 27.54 | 9.19e-05 2.41 7.11e-15
96 | 4.81e-05 36.78 | 9.87e-04 1.79 1.78e-14
144 | 1.46e-04 40.82 | 3.36e-03 1.78 2.84e-14
192 | 5.79e-04 24.44 | 8.46e-03 1.67 3.55e-14
240 | 7.41e-04 37.32 | 1.76e-02 1.57 5.68e-14
288 | 1.06e-03 45.07 | 2.90e-02 1.65 1.71e-13
336 | 1.65e-03 45.99 | 4.48e-02 1.69 2.27e-13
384 | 2.43e-03 46.61 | 1.60e-01 0.71 2.70e-13
432 | 4.82e-03 33.43 | 9.61e-02 1.68 2.84e-13
480 | 6.59e-03 33.57 | 1.53e-01 1.44 3.69e-13
And the following figure compares all of the six loop orderings for square matrices filled with Float64 numbers:
