28) Parallel reductions with CUDA.jl

Last time:

• Memory management with CUDA.jl

• Simple kernels using global memory

• Simple kernels using shared/local memory

• Instruction Level Parallelism

• Bank Conflicts

Today:

1. Outline

2. Parallel reduction on the GPU

3. Parallel reduction complexity

4. Different strategies for optimization

1. Outline

In this lecture, we will use an efficient parallel reduction on the GPU as an example to talk about:

• communication across thread blocks

• global synchronization problem across thread blocks

• use of different memory pools for optimization strategies

Note

References:

• We will losely follow Optimizing Parallel Reduction in CUDA by Mark Harris. Note that some of our kernels will be different than those given in the talk, but the ideas are (mostly) the same.

2. Parallel reduction on the GPU

We want to perform a Parallel Reduction operation on an array of size \(N\).

This is a common and important data parallel primitive. It should be:

• Easy to implement in CUDA

• But often harder to get it right

• We can use this as a great optimization example

Basic idea

• Tree-based approach used within each thread block

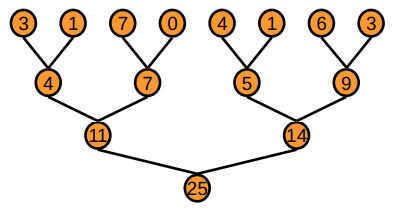
• Need to be able to use multiple thread blocks

  • to process very large arrays

  • to keep all multiprocessors on the GPU busy

  • each thread block reduces a portion of the array

• But how do we communicate partial results between thread blocks?

Problem: Global Synchronization

• If we could synchronize across all thread blocks, we could easily reduce very large arrays:

  • global sync after each block would produce its result

  • once all blocks reach sync, we would continue recursively

• But CUDA has no global synchronization. Why?

  • It’s expensive to build in hardware for GPUs with high processor count

  • It would force programmers to run fewer blocks (no more than # multiprocessors \(\times\) # resident blocks / multiprocessor) to avoid deadlock, which may reduce overall efficiency

Solution: decompose into multiple kernels.

• Kernel launch serves as a global synchronization point

• Kernel launch has negligible hardware overhead and low software overhead

Solution: Kernel Decomposition

• We avoid global sync by decomposing the computation into multiple kernel invocations

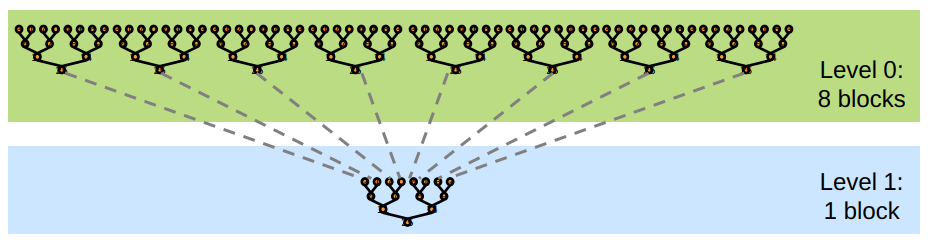
• In the case of reductions, the code for all levels is the same:

  • we have recursive kernel invocations

Measuring success: what are we striving for?

• We should strive to reach GPU peak performance

• But we need to choose the right metric to measure success:

  • GFLOP/s: for compute-bound kernels

  • Bandwidth: for memory-bound kernels

• Reductions have very low arithmetic intensity

  • 1 flop per element loaded (bandwidth-optimal)

• Therefore we are not compute-bound, hence we should strive for peak bandwidth

3. Parallel reduction complexity

• \(\log(N)\) parallel steps, each step \(S\) does \(N/2^S\) independent operations

  • Step complexity is \(O(\log N)\)

• For \(N=2^D\) (we are sticking to power-of-2 block sizes), performs \(\Sigma_{S \in [1, \dots, D]} 2^{D-S} = N-1\) operations

  • Work complexity is \(O(N)\) - It is work-efficient, i.e., does not perform more operations than a sequential algorithm

• With \(P\) threads physically in parallel (\(P\) processors), time complexity is \(O(\frac{N}{P} + \log N)\)

  • Compare to \(O(N)\) for sequential reduction

  • In a thread block, \(N=P\), so \(O(\log N)\)

4. Different strategies for optimization

The code for the Julia GPU reduction can be found in julia_codes/module8-3/reduction.jl

Basic implementation idea:

Version 1

Because there is no global synchronization, we need to launch the kernel multiple times in thread blocks (work groups).

In each launch, each thread block will work together to reduce the set of numbers to a single summed value.

• In the first iteration we launch, say, num_groups (8 by default in the kernel below) work groups to reduce a vector of length N to a vector of length num_groups.

• We will then recurse and reduce the vector of length num_groups to a smaller vector, and continue until we only have 1 element in the partially reduced vector.

"""
   reduction_knl_v1(x, y; op=+, ldim::Val{LDIM}=Val(256))

Basic interleaved memory access version where each `LDIM` chunk of values from `x`
are reduced using `op` (+ by default) to single values which are stored in the first
`gridDim().x` values of `y`

Problems:
  - Modulo is slow on the GPU >> Remove by calculating
  - threads in a warp are divergent (for the if statement) >> shift threads as algorithm progresses
"""
function knl_reduction_v1!(y, x, N, op, ::Val{LDIM}) where LDIM
  tid = threadIdx().x
  bid = blockIdx().x
  gid = tid + (bid - 1) * LDIM # global thread index
  l_x = @cuStaticSharedMem(eltype(x), LDIM) # shared memory allocation

  @inbounds begin
    # set the local/shared memory array
    if gid <= N
      l_x[tid] = x[gid]
    else
      l_x[tid] = 0
    end

    sync_threads()

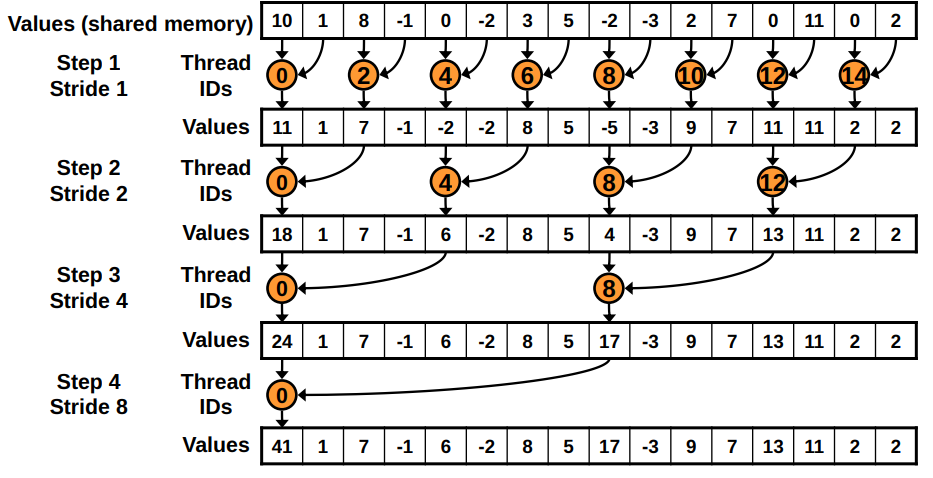
    s = 1
    while s < LDIM
      # I'm still active if my thread ID (minus 1) is divisible by 2*s
      if ((tid-1) % (2 * s) == 0)
        # combine my value to my (interleaved/strided) neighbors value
        l_x[tid] = op(l_x[tid], l_x[tid + s])
      end
      s *= 2
      sync_threads()
    end

    # Thread 1 is the only remaining "real" thread which will carry the result
    tid == 1 && (y[bid] = l_x[tid])
  end

  nothing
end

Problems:

1. Modulo (%) is very slow

2. Highly divergent warps are very inefficient. We have an if-statement for which, at the first step, half of the threads in a warp will be idleing; in subsequent steps, even more will be idleing

Version 2

• Work-group (block size) sized elements of the given array into shared memory (as in version 1)

• Use binary sum to reduce the values to a single number (as in version 1)

• Recurse until there is only one group (as in version 1)

• BUT: replace divergent branch in inner loop, with strided index and non-divergent branch

"""
   reduction_knl_v2(x, y; op=+, ldim::Val{LDIM}=Val(256))

Improved strided memory access version where each `LDIM` chunk of values from `x`
are reduced using `op` to single values which are stored in the first
`gridDim().x` values of `y`

Problems:
  - Memory access is still strided, thus bank conflicts >> sequential access
"""
function knl_reduction_v2!(y, x, N, op, ::Val{LDIM}) where LDIM
  tid = threadIdx().x
  bid = blockIdx().x
  gid = tid + (bid - 1) * LDIM
  l_x = @cuStaticSharedMem(eltype(x), LDIM)

  @inbounds begin
    if gid <= N
      l_x[tid] = x[gid]
    else
      l_x[tid] = 0
    end

    sync_threads()

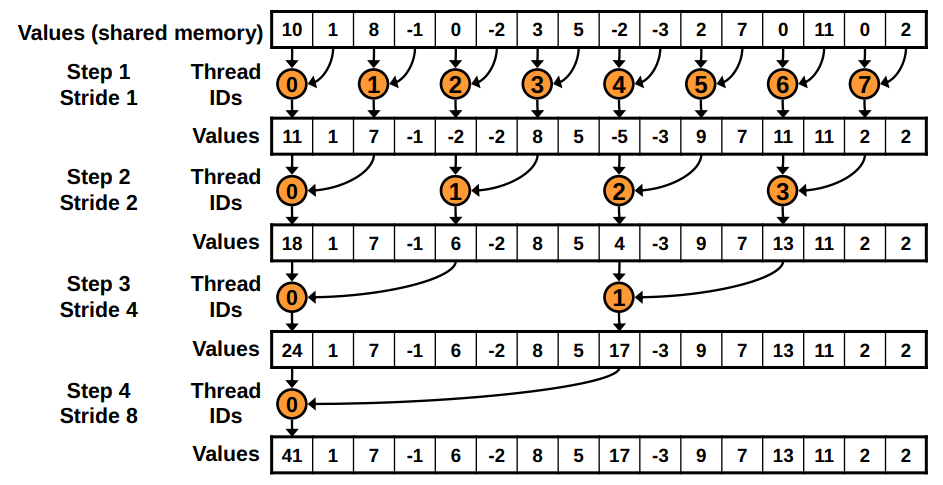
    s = 1
    while s < LDIM
      # figure out whether I'm in the active block
      sid = 2 * (tid-1) * s + 1
      if sid + s <= LDIM
        # combine my value to my (strided) neighbors value
        l_x[sid] = op(l_x[sid], l_x[sid+s])
      end
      s *= 2
      sync_threads()
    end

    # Thread 1 is the only remaining "real" thread
    tid == 1 && (y[bid] = l_x[tid])
  end

  nothing
end

Observations:

• Note: In the graphics, version 2 has sequential thread IDs instead of chosing theads based on if they are divisible by \(2*s\) (where \(s\) is the step number) as in version 1.

Problem:

• New Problem: Shared Memory Bank Conflicts!

Version 3

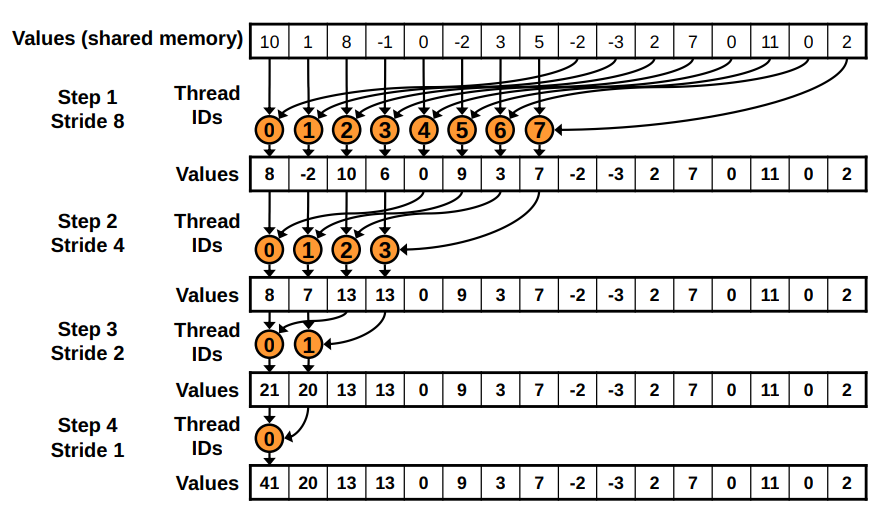
• Use sequential addressing of main memory

• This version with sequential addressing is conflict free (i.e., no bank conflicts)

• We replace strided indexing in inner loop, with reversed loop and threadID-based indexing

"""
   reduction_knl_v3(x, y; op=+, ldim::Val{LDIM}=Val(256))

Basic sequential memory access version where each `LDIM` chunk of values from
`x` are reduced using `op` to single values which are stored in the first
`gridDim().x` values of `y`

Problems:
  - Some threads do very little work (idle threads) >> have each thread add in a few values
"""
function knl_reduction_v3!(y, x, N, op, ::Val{LDIM}) where LDIM
  tid = threadIdx().x
  bid = blockIdx().x
  gid = tid + (bid - 1) * LDIM
  l_x = @cuStaticSharedMem(eltype(x), LDIM)

  @inbounds begin
    if gid <= N
      l_x[tid] = x[gid]
    else
      l_x[tid] = 0
    end

    sync_threads()

    # bit right shift to divide by 2
    s = LDIM >> 1
    while s > 0
      # I'm still active if my thread ID is less than
      if tid <= s
        # combine my value to my (strided) neighbors value
        l_x[tid] = op(l_x[tid], l_x[tid + s])
      end
      # bit right shift to divide by 2
      s = s >> 1
      sync_threads()
    end

    # Thread 1 is the only remaining "real" thread
    tid == 1 && (y[bid] = l_x[tid])
  end

  nothing
end

Problem

• Half of the threads are idle on first loop iteration! This is wasteful

Version 4

• First add during load: Let each thread load OVERLAP numbers and add them together before switching to shared memory.

"""
   reduction_knl_v4(x, y; op=+, ldim::Val{LDIM}=Val(256))

Add a few values before switching to shared memory with sequential memory
access version where each `LDIM` chunk of values from `x` are reduced using
`op` to single values which are stored in the first `gridDim().x` values of `y`
"""
function knl_reduction_v4!(y, x, N, op, ::Val{LDIM},
                           ::Val{OVERLAP}) where {LDIM, OVERLAP}
  tid = threadIdx().x
  bid = blockIdx().x
  gid = tid + (bid - 1) * LDIM
  gsz = LDIM * gridDim().x # total number of threads

  l_x = @cuStaticSharedMem(eltype(x), LDIM)

  @inbounds begin
    # Have each thread initially load and add OVERLAP values
    p_x = zero(eltype(x))
    for n = 1:OVERLAP
      if gid + (n-1) * gsz <= N
        p_x += x[gid + (n-1)*gsz]
      end
    end

    l_x[tid] = p_x

    sync_threads()

    # bit right shift to divide by 2
    s = LDIM >> 1
    while s > 0
      # I'm still active if my thread ID is less than
      if tid <= s
        # combine my value to my (strided) neighbors value
        l_x[tid] = op(l_x[tid], l_x[tid + s])
      end
      s = s >> 1 # bit right shift to divide by 2 again
      sync_threads()
    end

    # Thread 1 is the only remaining "real" thread
    tid == 1 && (y[bid] = l_x[tid])
  end

  nothing
end