23) Collective communication

23) Collective communication#

Last time:

  • Blocking and non-blocking point-to-point communications

Today:

  1. MPI Collective Communication

  2. Minimum Spanning Trees

1. MPI Collective Communication#

Tip

Resources for the lecture:

  1. Article: Chan et al., Collective communication: theory, practice, and experience

  2. Lecture Notes from the University of Texas at Austin: Robert van de Geijn (RVDG) Collective Communication: Theory and Practice

In the previous lecture we considered point-to-point communication, that is communication between two MPI ranks. In this lecture we will consider communication that involves all the ranks in a communicator.

Reductions#

Recall that reductions are a case of collective communication operations.

An operator is a reduction operator if:

  1. It can reduce an array to a single scalar value.

  2. The final result should be obtainable from the results of the partial tasks that were created.

These two requirements are satisfied for commutative and associative operators that are applied to all array elements.

Example#

Suppose we have an array \(x = [1,2,3,4,5,6,7,8]\). The sum of this array can be computed serially by sequentially reducing the array into a single sum using the + operator.

Starting the summation from the beginning of the array yields:

\[ (((((((1 + 2) + 3) + 4) + 5) + 6) + 7) + 8) \]

Since + is both commutative and associative, it is a reduction operator. Therefore this reduction can be performed in parallel using several processes/cores, where each process/core computes the sum of a subset of the array, and the reduction operator merges the results.

Using a binary tree reduction would allow \(4\) processes/cores to compute

\[ \underbrace{ \underbrace{ \underbrace{(1 + 2)}_{p_0} + \underbrace{(3 + 4)}_{p_1}}_{p_0} + \underbrace{ \underbrace{(5 + 6)}_{p_1} + \underbrace{(7 + 8)}_{p_3}}_{p_1} }_{p_0} \]

So a total of \(4\) cores can be used to compute the sum in \(\log_n \equiv \log_2 8 = 3\) steps instead of the \(7\) steps required for the serial version.

Of course the result is the same, but only because of the associativity of the reduction operator. The commutativity of the reduction operator would be important if there were a master core distributing work to several processors, since then the results could arrive back to the master processor in any order. The property of commutativity guarantees that the result will be the same.

  • From Fig. 1 in Chan et al.

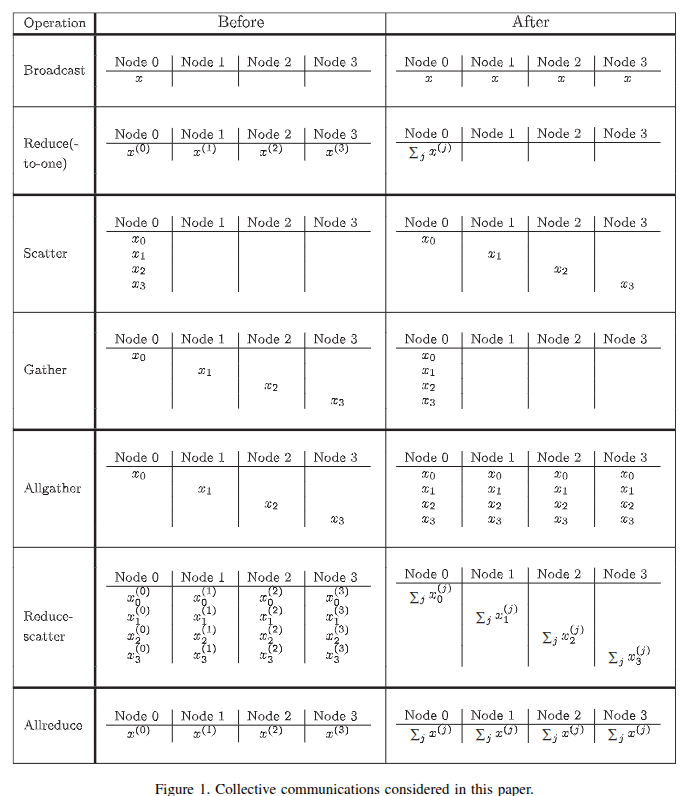
Figure 1 of Chang et al, Collective communication: theory, practice, and experience article

Types of possible collective communication:

  • Broadcast: one rank sends data to all the other ranks (RVDG: 93, MPI_Bcast)

  • Reduce(-to-one): Combine (e.g., sum, max/min, etc.) information from all ranks to one rank (RVDG: 94, MPI_Reduce)

  • Scatter: One rank send data to all other ranks (RVDG: 96, MPI_Scatter)

  • Gather: All ranks send data to one rank (RVDG: 97, MPI_Gather)

  • Allgather: All ranks sends information to all ranks (RVDG: 99, MPI_Allgather)

  • Reduce-scatter: Reduce and scatter out the reduced result (RVDG: 101, MPI_Reduce_scatter)

  • Allreduce: All ranks combine information from all ranks and the result is available to all ranks (RVDG: 102, MPI_Allreduce)

Note that there are pairs of reciprocal/dual operations:

  • Broadcast/Reduce(-to-one) (RVDG: 95)

  • Scatter/Gather (RVDG: 98)

  • Allgather/Reduce-scatter (RVDG: 101)

Allreduce is the only operationthat does not have a dual (or it can be viewed as its own dual).

Two broad classes of collective operations (Chan et al., 1752):

  • Data redistribution operations: Broadcast, scatter, gather, and allgather. These operations move data between processors.

  • Data consolidation operations: Reduce(-to-one), reduce–scatter, and allreduce. These operations consolidate contributions from different processors by applying a reduction operation. We will only consider reduction operations that are both commutative and associative.

2. Minimum Spanning Trees (MST)#

2.1 Broadcast#

We want to perform a broadcast operation, i.e., we want to send a message from a root rank to all ranks.

Naive Algorithm#

A naive broadcast just has the root send the message to each rank.

You can find the following code at julia_codes/module6-3/naivebcast.jl.

 1# Naive broadcast just has the root send the message to each rank
 2function naivebcast!(buf, root, mpicomm)
 3  # Figure out who we are
 4  mpirank = MPI.Comm_rank(mpicomm)
 5
 6  # If I am the root send the message to everyone
 7  if mpirank == root
 8    # How many total ranks are there
 9    mpisize = MPI.Comm_size(mpicomm)
10
11    # Create an array for the requests
12    reqs = Array{MPI.Request}(undef, mpisize)
13
14    # Loop through ranks and send message
15    for n = 1:mpisize
16      # MPI uses 0 based indexing for ranks
17      neighbor = n-1
18
19      # If its me jst set my request to NULL (e.g., no-op)
20      if neighbor == mpirank
21        reqs[n] = MPI.REQUEST_NULL
22      else # otherwise send message to neighbor
23        reqs[n] = MPI.Isend(buf, neighbor, 7, mpicomm)
24      end
25    end
26    # Wait on all the requests
27    MPI.Waitall!(reqs)
28  else # Since we are not the root, we receive
29    MPI.Recv!(buf, root, 7, mpicomm)
30  end
31end

And the following testing code at julia_codes/module6-3/naivebcast_test.jl.

 1using MPI
 2include("naivebcast.jl")
 3
 4let
 5  # Initialize MPI
 6  MPI.Init()
 7
 8  # store communicator
 9  mpicomm = MPI.COMM_WORLD
10
11  # Get some MPI info
12  mpirank = MPI.Comm_rank(mpicomm)
13  mpisize = MPI.Comm_size(mpicomm)
14
15  # Divide all ranks halfway to determine the root
16  root = div(mpisize, 2) # Integer division
17
18  # create buffer for the communication
19  buf = [mpirank]
20
21  # have root broadcast message to everyone
22  naivebcast!(buf, root, mpicomm)
23
24  # check to make sure we got back the right message
25  @assert buf[1] == root
26
27  MPI.Barrier(mpicomm)
28  time = @elapsed begin
29    naivebcast!(buf, root, mpicomm)
30    MPI.Barrier(mpicomm)
31  end
32
33  # Let's print the execution time:
34  # Short hand for:
35  #=
36  if mpirank == 0
37    print("Execution time: ", time,"\n")
38  end
39  =#
40  mpirank == 0 && print("Execution time: ", time,"\n")
41
42  # shutdown MPI
43  MPI.Finalize()
44end

Minimum Spanning Tree Algorithm#

See Chan et al. Fig. 3(a) & Fig 4(a); RVDG pages 108-171.

You can find the following code at julia_codes/module6-3/mstbcast.jl.

 1# Example implementation of MSTBcast (Fig. 3(a)) from
 2# Chan, E., Heimlich, M., Purkayastha, A. and van de Geijn, R. (2007),
 3# Collective communication: theory, practice, and experience. Concurrency
 4# Computat.: Pract. Exper., 19: 1749–1783. doi:10.1002/cpe.1206
 5#
 6# In this minimum spanning tree (mst) broadcast algorithm:
 7#   - Divide ranks into two (almost) equal group
 8#   - root sends data to one rank in other group (called the dest)
 9#   - recurse on two groups with root and dest being the "roots" of respective
10#     groups
11#
12#  For nine ranks with root = 1 the algorithm would be (letters just represent
13#  who sends/recvs data)
14#
15#  0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8
16#  ---------------------------------
17#    | x |   |   |   |   |   |   |
18#    | a |   |   |   |   |   |   | a  1->8
19#    | a |   |   | a |   | b |   | b  1->4, 8->6
20#    | a | a | c | c | d | d | b | b  1->2, 4->3, 6->5, 8->7
21#  a | a | x | x | x | x | x | x | x  1->0
22function mstbcast!(buf, root, mpicomm;
23                   left = 0, right = MPI.Comm_size(mpicomm)-1)
24
25  # If there is no one else, let's get outta here!
26  left == right && return
27  # Short hand for:
28  #=
29  if left == right
30    return
31  end
32  =#
33
34  # Determine the split
35  mid = div(left + right, 2) # integer division
36
37  # Whom do I send to?
38  dest = (root <= mid) ? right : left
39  # Short hand for:
40  #=
41  if root <= mid
42    dest = right;
43  else
44    dest = left;
45  end
46  =#
47
48  # Figure out who we are
49  mpirank = MPI.Comm_rank(mpicomm)
50
51  # If I'm the root or dest send or recv (respectively)
52  req = MPI.REQUEST_NULL
53  if mpirank == root
54    req = MPI.Isend(buf, dest, 7, mpicomm)
55  elseif mpirank == dest
56    MPI.Recv!(buf, root, 7, mpicomm)
57  end
58
59  # Recursion:
60  # I'm in the left group and the root is my new root
61  if mpirank <= mid && root <= mid
62    mstbcast!(buf, root, mpicomm; left=left, right=mid)
63  # I'm in the left group and the dest is my new root
64  elseif mpirank <= mid && root > mid
65    mstbcast!(buf, dest, mpicomm; left=left, right=mid)
66  # I'm in the right group and the dest is my new root
67  elseif mpirank > mid && root <= mid
68    mstbcast!(buf, dest, mpicomm, left=mid + 1, right=right)
69  # I'm in the right group and the root is my new root
70  elseif mpirank > mid && root > mid
71    mstbcast!(buf, root, mpicomm, left=mid + 1, right=right)
72  end
73
74  # Make sure all my sends are done before I get outta dodge
75  MPI.Wait!(req)
76end

And the following testing code at julia_codes/module6-3/mstbcast_test.jl.

 1using MPI
 2include("mstbcast.jl")
 3
 4let
 5  # Initialize MPI
 6  MPI.Init()
 7
 8  # store communicator
 9  mpicomm = MPI.COMM_WORLD
10
11  # Get some MPI info
12  mpirank = MPI.Comm_rank(mpicomm)
13  mpisize = MPI.Comm_size(mpicomm)
14
15  # Divide all ranks halfway to determine the root
16  root = div(mpisize, 2) # Integer division
17
18  # create buffer for the communication
19  buf = [mpirank]
20
21  # have root broadcast message to everyone
22  mstbcast!(buf, root, mpicomm)
23
24  # check to make sure we got back the right message
25  @assert buf[1] == root
26
27  MPI.Barrier(mpicomm)
28  time = @elapsed begin
29    mstbcast!(buf, root, mpicomm)
30    MPI.Barrier(mpicomm)
31  end
32
33  # Let's print the execution time:
34  # Short hand for:
35  #=
36  if mpirank == 0
37    print("Execution time: ", time,"\n")
38  end
39  =#
40  mpirank == 0 && print("Execution time: ", time,"\n")
41
42  # shutdown MPI
43  MPI.Finalize()
44end

Let’s compare them#

You can find the driver for the comparison code at julia_codes/module6-3/bcast_compare.jl.

 1using MPI
 2include("naivebcast.jl")
 3include("mstbcast.jl")
 4let
 5  # Initialize MPI
 6  MPI.Init()
 7
 8  # store communicator
 9  mpicomm = MPI.COMM_WORLD
10
11  # Get some MPI info
12  mpirank = MPI.Comm_rank(mpicomm)
13  mpisize = MPI.Comm_size(mpicomm)
14
15  # Divide all ranks halfway to determine the root
16  root = div(mpisize, 2) # Integer division
17
18  # create buffer for the communication
19  buf = [mpirank]
20
21  # have root broadcast message to everyone
22  mstbcast!(buf, root, mpicomm)
23  naivebcast!(buf, root, mpicomm)
24
25  mst_t1 = time_ns() # The time_ns() function in Julia returns the current time in nanoseconds
26  mstbcast!(buf, root, mpicomm)
27  mst_t2 = time_ns()
28  nve_t1 = time_ns()
29  naivebcast!(buf, root, mpicomm)
30  nve_t2 = time_ns()
31
32  mpirank == 0 && print("Elapsed time for the naive algorithm: \n")
33  mpirank == 0 && @show (nve_t2 - nve_t1) * 1e-9
34  mpirank == 0 && print("Elapsed time for the mst algorithm: \n")
35  mpirank == 0 && @show (mst_t2 - mst_t1) * 1e-9
36
37  # shutdown MPI
38  MPI.Finalize()
39end

Minimum Spanning Tree Reduce?#

For a Minimum Spanning Tree (MST) Reduce see See Chan et al. Fig. 3(b) & Fig. 4(b); RVDG pages 172-184.

  • Note: It’s possible to write the mstbcast (and a corresponding MST reduce version) without recursion (although we won’t see it in this class) and doing it with blocking communication is easier than non-blocking…

Contents